26 - FILOSOFIA E MATEMÁTICA /TEOREMA DE TALES USADO NA ODONTOLOGIA

Autor:
Santos, Alfredo A.
Graduado em Odontologia - FO-UFBA.
Licenciado em Desenho e Artes Plásticas - EBA-UFBa.
Especialista em Critica de Artes - EBA-UFBA.
Especialista em Ortodontia e Ortopedia Maxilar - UCCB.
Especialista em Radiologia e Imaginologia FO -UFBA.
Especialista em Microbiologia - FACCEBA.
Pós graduado em Implantodontia - ABO-MOC.
Pós Graduação em Administração em Saúde Pública - UNAERP.
Pós Graduação em Comunicação e Jornalismo - UESB.
Membro Titular do Colégio Brasileiro de Implantodontia (CBI).





O QUE É UM TEOREMA.

Teorema é um termo introduzido por Euclides, em Elementos, para significar "afirmação que pode ser provada". Em grego, originalmente significava "espetáculo" ou "festa". Atualmente, é mais comum deixar o termo "TEOREMA" para apenas certas afirmações que podem ser provadas e de grande "importância matemática", o que torna a definição um tanto subjetiva.
Provar teoremas é a principal atividade dos matemáticos.
É importante notar que "teorema" é diferente de "teoria".
Para se produzir um teorema é preciso demonstrá-lo (i.e., prová-lo), por mais que a demonstração em si não faça parte do teorema (um teorema consiste em apenas uma implicação que pode ser provada). Obviamente, um teorema pode ter mais de uma única demonstração.
Já uma teoria é um conjunto de construções, definições e proposições interrelacionadas que apresenta uma visão sistemática dos fenómenos através de uma especificação de relações entre variáveis com o objectivo de explicar e prever os fenómenos".Ou seja, uma teoria:
(a) deve explicar os fatos observados. (do modo mais simples possível e como ele é)
(b) deve ser consistente com outro(s) corpo(s) de conhecimento e deve fornecer meios
para a sua verificação.
(c) deve ser útil. (uma teoria é um modelo).

A idéia de que afirmações verdadeiras precisam ser provadas, e gera um problema cíclico: a própria prova para determinada afirmação deve ser verdade.
Mas, para que seja aceita como verdadeira neste contexto, será necessária uma prova irrefutável ou seja para ela, uma prova para a própria prova.
Isso se resolve tomando algumas afirmações como verdades a priori, as chamadas hipóteses do teorema (veja que hipótese aqui é bem diferente de conjectura, abaixo).
Chamamos o conjunto das afirmações concluídas (ou seja, aquilo que efetivamente é provado) de tese. O Teorema é, assim, a implicação das hipóteses na tese. É importante aqui ressaltar que as regras de inferência devem fazer parte das hipóteses.
É extremamente comum agrupar várias hipóteses tidas como verdadeiras numa teoria, definido-se como qualquer outra verdade, dentro da teoria, uma implicação destas. Neste caso, tais hipóteses são classificadas ou como axiomas (ou postulados, este último nome mais usado em teorias em Ciências Naturais) ou como definições. As definições são aquelas usadas para reservar palavras, fixando o seu sentido, e os axiomas tratam das relações entre os termos reservados. Para que uma teoria possa ser construída devem haver palavras reservadas aceitas sem definição (os chamados entes primitivos), cujo significado formalmente virá de acordo com os axiomas (o exemplo mais clássico de ente primitivo é "ponto", como usado por Hilbert em Grundlagen der Geometrie (Bases de geometria)). Numa teoria axiomática, apenas as hipóteses novas (que não são axiomas) são apresentadas no enunciado de um teorema.
Deve se notar, também, que o modo que a inferência lógica é feita (o porque de cada "salto" dado entre cada passo da demonstração) faz parte das hipóteses (ou pelo menos algum conjunto de hipóteses que implique nos "saltos" dados), formalmente falando. Em geral esse conjunto de hipóteses que nos fornecem os "saltos" são os axiomas da lógica usada.
Dentro do estudo de Lógica Matemática, o ramo que investiga as demonstrações é chamado Teoria da Prova.
O resultado mais famoso desta é o Teorema da Incompletude de Gödel, o qual afirma que, dentro de certas hipóteses muito razoáveis, em toda teoria axiomática consistente (i.e., sem contradições lógicas) existem afirmações que não são nem verdades nem mentira dentro da teoria, no sentido de que caso alguma delas for considerada um novo axioma, ou caso sua negação for considerada um novo axioma, a teoria continuará consistente. Usualmente deixa-se o termo "teorema" apenas para as afirmações que podem ser provadas de grande importância. Assim, são dados outros nomes para os outros tipos dessas afirmações:

• Proposição: é uma sentença não associada a algum outro teorema, de simples prova e de importância matemática menor.

• Lema: é um "pré-teorema", um teorema que serve para ajudar na prova de outro teorema maior. A distinção entre teoremas e lemas é um tanto quanto arbitrária, uma vez que grandes resultados são usados para provar outros. Por exemplo, o Lema de Gauss e o Lema de Zorn são muito interessantes de per se, e muitos autores os denominam de Lemas, mesmo que não os usem para provar alguma outra coisa.

• Corolário: é uma conseqüência direta de outro teorema ou de uma definição, muitas vezes tendo suas demonstrações omitidas, por serem simples.
Outros termos menos importantes e menos rigoroso, usados quando não se quer usar a palavra teorema.
• Regra. Regra é algo que alguém superior impõe pra a sociedade respeitar.

• Lei, que também pode se referir a axiomas, regras de dedução e a distribuições de Probabilidade. Lei pode ser: a). Lei, uma regra jurídica que permite, proíbe ou obriga uma conduta humana. b). Lei (ciências), uma regra científica que descreve um fenômeno que ocorre com certa regularidade. C). Lei, uma comuna italiana.

• Princípio. Irei tratar do princípio ético.

É o ponto do qual partem suas opiniões, pensamentos e ações, tendo definido o seu princípio tudo o mais será produto do mesmo. Vou demonstrar um exemplo prático: Se o principio de uma pessoa em questão é a paz ela tende a ter pensamentos e atos pacíficos, o pacifismo ocupara o papel de destaque em suas opiniões. Essa linha de pensamento é valida para todos os demais princípios: políticos, religiosos, artísticos e etc.

• Algoritmo: Um algoritmo (palavra derivada do nome de um matemático Persa Al-Khwarizmi), é um conjunto finito de instruções bem definidas para a realização de uma tarefa na qual, dado um estado inicial, conduzirá para um estado final correspondente reconhecível (em contraste com heurística). Os algoritmos podem ser implementados em um programa de computador, embora frequentemente de maneira restrita; um erro no projeto de um algoritmo para a solução de um problema pode levar a falhas no programa implementado.

A construção de algoritmos computacionais pode ser feita de diversas formas, e cada "forma" é chamada de linguagem. Essa linguagem pode ser em forma de texto, números, fórmulas, ou gráfico. O produto de uma linguagem é chamado de código, que define o comportamento do computador para a resolução de problemas. Métodos de construção desses códigos também são estudados na Ciência da Computação. Desenvolver esses códigos pode ser também considerado uma arte e se parecer com qualquer produto artístico de outra área do conhecimento humano.

Geralmente, algoritmos são escritos em uma linguagem próxima à da linguagem natural, ou seja, uma linguagem mais facilmente compreendida por um ser humano do que por um computador. Algoritmos podem ser implementados em várias linguagens de programação.

• Paradoxo São denominações usadas quando a afirmação vai aparentemente de encontro com alguma outra verdade ou com alguma noção intuitiva. Entretanto, tal termo também pode ser usado para afirmações falsas que aparentem ser verdadeiras em um primeiro momento.

• Conjecturas são denominações dadas a alguns teoremas continuam a ser chamados de logo após serem provados (por exemplo, a Conjectura de Poincaré).
O termo conjectura é usado para afirmações que não se sabe se são verdadeiras, e que acredita-se que são verdadeiras, mas nunca ninguém conseguiu prová-las nem negá-las (as vezes conjecturas são chamadas de hipóteses (como em Hipótese de Riemann), obviamente, num sentido diferente do aqui já descrito).

• Axioma.é uma sentença ou proposição que não é provada ou demonstrada e é considerada como óbvia ou como um consenso inicial necessário para a construção ou aceitação de uma teoria. Por essa razão, é aceito como verdade e serve como ponto inicial para dedução e inferências de outras verdades (dependentes de teoria).
Na matemática, um axioma é uma hipótese inicial de qual outros enunciados são logicamente derivados. Pode ser uma sentença, uma proposição, um enunciado ou uma regra que permite a construção de um sistema formal. Diferentemente de teoremas, axiomas não podem ser derivados por princípios de dedução e nem são demonstráveis por derivações formais, simplesmente porque eles são hipóteses iniciais. Isto é, não há mais nada a partir do que eles seguem logicamente (em caso contrário eles seriam chamados teoremas). Em muitos contextos, "axioma", "postulado" e "hipótese" são usados como sinônimos.

01. Teorema de Tales.

O Teorema de Tales foi proposto pelo filósofo grego Tales de Mileto, e afirma que: quando duas retas transversais cortam um feixe de retas paralelas, as medidas dos segmentos delimitados pelas transversais são proporcionais. Para entender melhor o Teorema de Tales, é preciso saber um pouco sobre razão e proporção. Para a resolução de um problema envolvendo o Teorema de Tales, utiliza-se a propriedade fundamental da proporção, multiplicando-se os meios pelos extremos. Considerando-se o exemplo da figura, tem-se:





Aplicações do Teorema de Tales.
O Teorema de Tales pode ser aplicado em triângulos que possuem uma reta paralela a um dos lados.





Esquema mostrando validade do Teorema de Tales.






USO DO TEOREMA DE TALES EM ODONTOLOGIA.
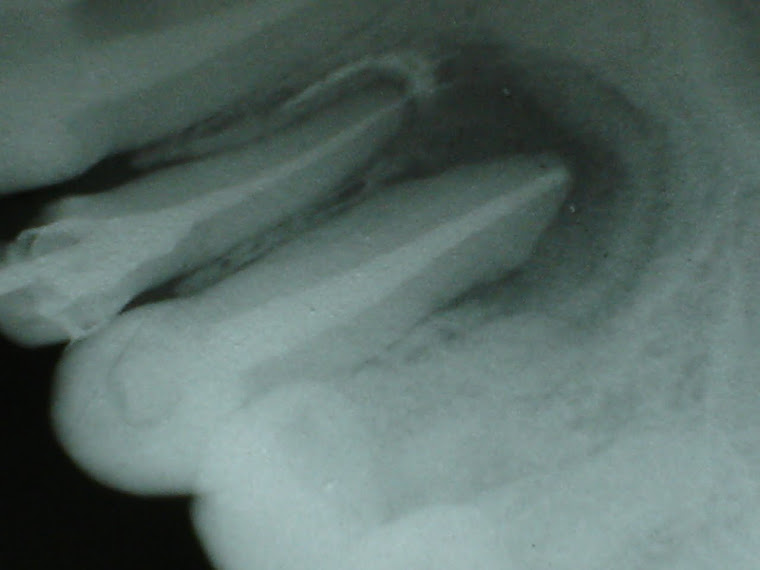
O Teorema de Tales e usado na Odontometria Endodôntica ou seja na medida dos canais Radiculares. Coloca-se um limitador (cursor ou "stop") no instrumento para demarcar o comprimento que será introduzido no canal radicular (CRI) Comprimento Real do Instrumento. Esse cursor deverá apoiar-se na porção incisal ou oclusal do dente (ponto de referência) com a finalidade de se obter a mensuração do mesmo.
a) Radiografa-se o dente com o instrumento em posição intra canal. Feito isso, retira-se o instrumento e, para confirmar a medida estipulada anteriormente (CRI), mede-se a distância que vai da ponta do instrumento até o cursor ou seja o stop.
b) Uma vez processada a radiografia, mede-se o comprimento aparente do instrumento (CAI) e o comprimento aparente do dente (CAD), que nada mais são do que os comprimentos do instrumento e do dente vistos na radiografia, respectivamente. O CAI deve ser medido da ponta do instrumento até o ponto de referência onde o cursor foi apoiado.
c) Conhecidos o CRI, o CAI e CAD, podemos calcular o comprimento real do dente (CRD) aplicando a seguinte fórmula:
CRD = CRI x CAD / CAI
d) Uma vez obtido o CRD pode-se determinar o comprimento de trabalho (CT), que o comprimento real do dente menos 1 mm. Onde podemos obturar o canal radicular.
e) A seguir, verifica-se se o comprimento de trabalho (CT) obtido está correto, fazendo-se uma radiografia com o instrumento no interior do canal radicular no CT obtido. A análise da radiografia de confirmação do CT deve mostrar claramente o instrumento no interior do canal radicular colocado 1 mm aquém do ápice radiográfico. Caso essa situação não ocorra, deve-se iniciar a odontometria novamente. Pois está errada a odontometria. Atualmente aparelhos modernos de ultra-sonografia endodôntica, utilizam deste teorema para a odontometria, sem radiografias. Portanto mulheres grávidas podem submerter-se à intervenção cirúrgicas dos canais dentário. Estes aparelhos são contruidos de três formas: a) Localizadores tipo resistência (Corrente Continua), a utilização da corrente continua na medição da resistência elétrica. Leituras a partir de um eletrodo positivo e outro negativo fechando o circuito.
b) Localizadores tipo Impedância (Corrente Alternada)leituras feitas ha partir de altas frequências.
c) Localizadores tipo Frequência (Corrente alternada e outras duas frequências)mede-se com a utilização de duas frequências de corrente alternada para medição da diferença ou quociente entre as duas impedancias.


Bibliografia consultada:

01 - www.mat.uc.pt/~jaimecs/euclid/elem.html - Edição de 1855.
02 - pt.wikipedia.org/wiki/Teorema_de_Tales.
03 - pt.wikibooks.org/.../Teorema_de_Tales:
04 - www.cienciamao.if.usp.br/tudo/t2k.php.
05 - pt.wikipedia.org/wiki/Odontometria .
06 - www.endodontia.com.br/index_arquivos/Justy%20II.pdf.
07 - www.endo-e.com/odontometria.htm
08 - bases.bireme.br/.../online.
09 - www.forp.usp.br/restauradora/metria.htm.
10 - www.patologiaoral.com.br/endo/odontometria.
11 - www.endodontia.com.br/
12 - www.forp.usp.br/restauradora/metria.htm