
AUTOR:
SANTOS,Alfredo.A.
Graduado em Odontologia - FO-UFBa.
Licenciado em Desenho e Artes Plásticas - EBA-UFBa.
Pós Graduado Lato Sensu em Ortodontia e Ortopedia Facial - UCCB.
Especialização em Critica de Artes - EBA-UFBA.
Especialista em Radiologia e Imaginologia - FO-UFBA.
Especialista em Microbiologia - FACCEBA.
Especialista em Administração Hospitalar - UNAERP.
Pós Graduado em Implantodontia - ABO-MOC.
Pós Graduado em DTM e DORF - CEBEO.
Pós Graduado em Eletromiografia de Face - MYO-TRONICS (USA).
Membro Titular do Colégio Brasileiro de Implantodontia - CBI.
Ex-Professor de Anatomia Artística - ICS-UFBA.
Biometria é a Ciência que trata da aplicação e do desenvolvimento de métodos e modelos estatísticos para a análise de dados em sistemas biológicos tais como o corpo humano.
Biometria [bio (vida) + metria (medida)] é o estudo estatístico das características físicas ou comportamentais dos seres vivos.
Para outros é um ramo da ciência que estuda a mensuração dos seres vivos. É a parte da Estatística que investiga atributos biológicos quantitativos.
È o estudo estatístico das características físicas ou comportamentais dos seres vivos. Recentemente este termo também foi associado a medida de características físicas ou comportamentais das pessoas como forma de identificá-las unicamente. Hoje a biometria é usada na identificação criminal, controle de ponto, controle de acesso, etc. Os sistemas chamados biométricos podem basear seu funcionamento em características de diversas partes do corpo humano, por exemplo: os olhos, a palma da mão, as digitais do dedo, a retina ou íris dos olhos. A premissa em que se fundamentam é a de que cada indivíduo é único e possuí características físicas e de comportamento (a voz, a maneira de andar, etc.) distintos.
Desde a antiguidade Artistas Plásticos e pintores usavam da geometria e da matemática para calcular e pintar suas telas, baseados na geometria. Este número é o principal elo de ligação entre as ciências exatas e as artes , pois é chamado de número mágico,
Antes e depois do renascimento Italiano, mestres da pintura, já usavam da matemática e geometria em suas telas.

Fig. 1. Mona Lisa.
Mona Lisa,com seu sorriso enigmático, um dos quadros mais famosos do mundo, pintado por Leonardo da Vinci e terminado em 1507, respeita várias proporções áureas: a cabeça e o torso da modelo cabem num retângulo áureo e seu corpo e cabeça num triângulo áureo. Seu olho esquerdo divide o quadro ao meio, dando-lhe a dimensão psicólogica que o tornou imortal. Para Leonardo Da Vinci, a natureza obedece regras ditadas pela matemática.
Cientistas usavam desta fórmula proporcional para determinar a natureza do crescimento e seu envolvimento com o crescimento biológico do animais
Na literatura há vários termos para descrever esta constante algébrica, tais como: Proporção áurea, proporção dourada, proporção divina, número de ouro, número dourado, divina proporção, proporção em extrema razão e ainda divisão de extrema razão.
Esta fórmula matemática, denotada pela letra grega φ(phi), esta expressão numérica equivalente ao número de valor arredondando as três casa decimáis,1,618.
Diferente do número Pi(π)3,142857…, (não confundir com o número Pi(π), quociente da divisão do comprimento de uma circunferência pela medida do seu respectivo diâmetro),

Fig. 2.
Fórmula de Euclides de Alexandria ( Matemático Grego):
Fi (Φ φ) PHI( 1 + 5 ½) 2. = 1,619033 sendo seu reciproco 0,618
O φ (phi) é uma constante matemática real algébrica irracional, envolvida no crescimento dos seres vivos, e por haver esta frequência é que o número de Ouro ganhou o status de número mágico.
A sequência do matemático Fibonacci tem as seguintes aplicações:
No Retângulo Áureo e o Nautilus,Triângulo de Pascal,Segmento Áureo,Ramos de troncos em árvores,Problema das Abelhas,Reflexão da luz: fibra Ótica,Filotaxia (Botânica),Pintura,Arte,Anatomia,Arquitetura,Indústria e Comércio,Dimensões áureas no homem,utilizados na física, Engenharia civil e Arquitetuta.
Veja os seguintes exemplos entre a natureza e a proporção Áurea.

Fig.3 - Sequência de Fibonaccio na construção do Nautilus Marinho.

Fig.4 - Concordância gráfica das curvas do Nautilus Marinho.

Fig.5 - Concordância das curvas do Nautilus Marinho(Búzio)na obtenção do aspiral.

Fig.6. Búzio Marinho.
A constante busca pela harmonia da face e dos dentes. Visto que, profissionais da Odontologia tem buscado na Geometria Harmônica subsídios para determinar um Canon Estético, ainda não encontrado e erradamente o chamam qualquer tipo de tratamento que envolve o material branco, o chamam de material estético, mesmo esquecendo da forma e função. O conceito Estético em Odontologia não obedem aos canones artísticos.
Esta fórmula foi criada na antiguidade por Euclides e usada por Leonardo da Vinci, Giotto, Paccioli e outros.
Euclides de Alexandria a denominou de “ Média e Extrema Razão”.
Leonardo da Vinci a denominou essa proporção de “ Secção Áurea “,
Klepler denominou por “ Secção ou proporção Divina”, Paccioli por “Proporção Divina”
Foi Euclides de Alexandria que no ano 300 A.C. descreveu a fórmula acima descrita (fig.2).
Nascido em 1175, Leonardo Pisano ou Leonardo de Pisa filho de Guglielmo Bonacci(Filho de Bonaccio) Fibonacci em 1202, observou que existe uma relação numérica áurea com a natureza desde a criação da natureza e a reprodução animal.
Descrevendo mais tarde a série Fibonacci.
Observando que havia uma co-relação entre a proporção áurea e toda a natureza, desde o corpo humano até os corpos celestes e marinhos do universo.
Observou que um número e sempre igual a soma de seus antecessores e que a divisão de um número pelo seu antecessor, tem como resultado um número áureo, 1,618.
Veja no exemplo a seguir: 0, 1,1,2, 3,5,8,13,21,34,55,89,144, 233,377.
Exemplo: Se dividirmos o numero 233 por 377 seu resultado seria 1,618033 e se somarmos: 1+1=2, 1+2= 3, 2+3 o resultado seria 5, 3+5= 8, e se tornaria uma série infindável.
Bem como se diminuirmos um número pelo seu antecessor será uma sequência lógica inversa: 377 - 233= 144, 233-144= 89, 144-89= 55, 89-55=34 e assim por diante.
Esta série chamamos de Série de Fibonacci.
APLICAÇÕES NA ODONTOLOGIA E ANATOMIA HUMANA
Em 1906, Berry criou o método da Proporção Biométrica que relacionava a coroa do incisivo central superior (ICS) corresponde a 1/16 da largura da face, sua altura corresponde 1/20 da altura do rosto pois Leonardo da Vinci já pintava figuras humanas baseado nesta peoporção. Outras partes do Corpo Humano tais como: a palma da mão corresponde a sua face até a altura do cabelo, o corpo humano é dividido em 7 cabeças e meia (o tamanho de sua cabeça), corresponde a altura do seu corpo (7,½).(Santos,Alfredo A.).

Fig. 7.
Homem Vitruviano - Leonardo da Vinci - 1490 AC.

Fig. 8.
Proporções Humanas.

fIG. 9.
Modulor - De Charles-Edouard Jeanneret - O Le Corbusier.
Em 1914, concluiu-se que os dentes humanos poderiam ser classificados em 3 formas distintas de acordo a face. Em Quadrado, Triangular e Ovóide. E que mudanças nessas formas estavam relacionada com a mistura racial de acordo seu rosto.
Em 1985, Mac Artur comparando as larguras mésio-distais do incisivos centais superiores (ICS) encontrou uma razão próxima a proporção Áurea.
A média dos incisivos inferiores segundo alguns autores e de 11,13 (± 1,27)e o valor Áureo calculado é de 10,96(± 0,98).
Os incisivos Superiores tiveram em média de 17,74 (± 1,58)e o valor calculado de 17,94 (± 1,99). Os valores encontrados ficaram próximos da proporção Áurea.
Altura do Incisivo Central Superior que tem 1,0 cm, na sua incisal deverá ter 1,618 que é um número áureo, já no Incisivo Lateral a largura será 60% menor equivalente à 1,0 cm.
Já para o canino será 0,618, vistos de frente ou em fotografias frontal, demonstra que os dentes artificiais não obedecem a esta regra.

Figura 10. Foto: LedinhaVC - Clinica Rádio.
Paciente classe III em norma lateral antes do tratamento Ortodôntico e Ortopédico dos Maxilares.

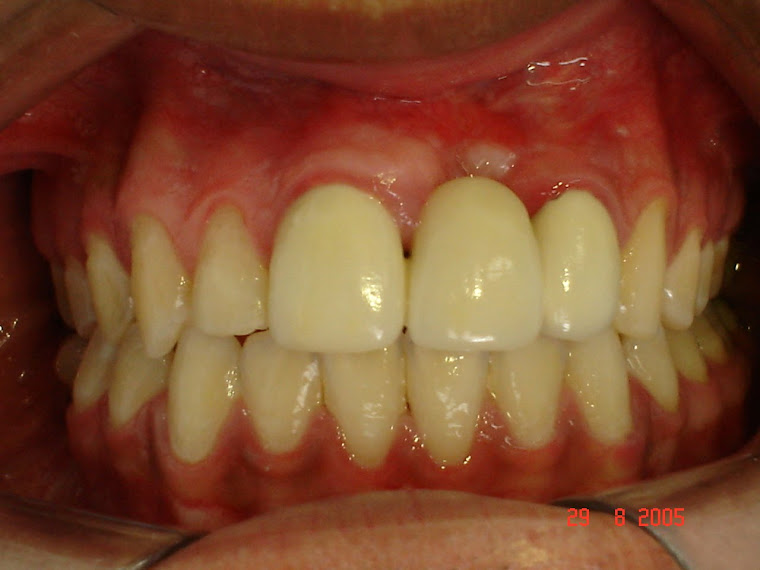
Figura 11.Foto: LedinhaVC - Clinica Rádio.
Paciente Classe III em norma frontal antes do tratamento Ortodôntico e Ortopédico dos Maxilares.

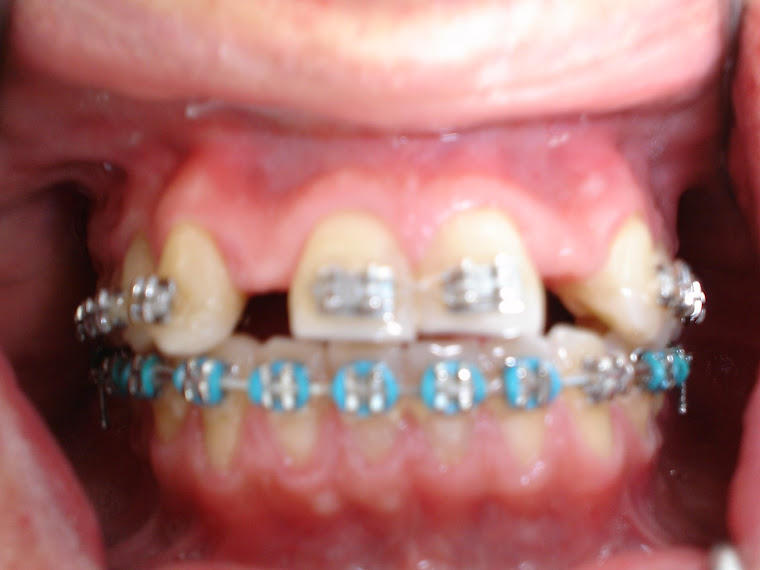
Figura 12. Foto: Alfredo Santos - Ortodontoclinica.
Paciente Classe III, pós tratamento Ortodôntico e Ortopédico dos Maxilares,
sem extração de dentes pré-molares ou redução Cirúrgica dos Maxilares.

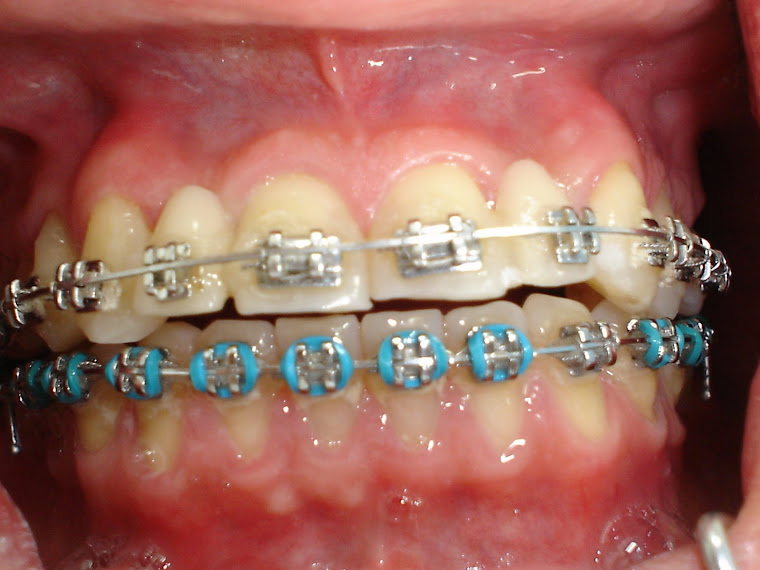
Figura 13. Foto: Alfredo Santos - Ortodontoclinica.
Paciente Classe III, pós tratamento Ortodôntico e Ortopédico dos Maxilares, sem redução cirúrgica - Baseado na série de Fibonaccio.
Em 1984, Tjan formulou uma norma padrão para fosse estabelecido um SORRISO ARTÍSTICO. Relacionando o tipo de sorriso, paralelismo da curva incisal do maxilar com o lábio inferior e o número de dentes que aparece no sorriso, método utilizado na confecção de prótese total ou na compra de dentes artificiais anteriores o que chamamos de 6 em curva. Já a medida do centro da íris até a comissura labial, corresponde a medida do filtro labial na base do nariz ao mento, para que determine a altura dos dentes de uma oclusão balanceada e harmônica, o que chamamos de dimensão vertical.
Estas medidas dos 6 dentes anteriores em curva expressa nas tabelas de fabricantes de dentes artificiais, faz com que o sorriso dos desdentados totais fique parecido com o sorriso artístico. E sua oclusão de certa forma balanceada ou ajustada de acordo com a forma do rosto e que modifica ou determina sua personalidade.
Em 1989, Bichara et All, disse estar havendo uma conscientização por parte dos ORTODONTISTAS, sobre a variação dos tamanhos dos dentes, exercem sobre a finalização dos casos. Baseado nesta assertiva as vezes precisamos apenas fazermos Slice (Desgastes Mesiais dos dentes) para concluirmos um caso.
Em 2006, Das Neves disse o seguinte: quanto mais próximos da proporção Áurea a face e os dentes da maxila, mais agradável será de se ver.
OUTRAS APLICAÇÕES:
Os números de Fibonacci são importantes para a análise em tempo real do algoritmo Euclidiano, para determinar o máximo divisor comum (MDC) de dois números inteiros.
Yuri Matiyasevich mostrou que os números de Fibonacci podem serem definidos por uma Equação Diofantina (Polinomiais com coeficientes inteiros) o que o levou à solução original do Décimo Problema de David Hilbert.
Os números de Fibonacci aparecem na fórmula das diagonais de um triângulo de Pascal (veja coeficiente binomial ou número binomial).
Um uso interessante da seqüencia de Fibonacci é na conversão de milhas para quilômetros. Por exemplo, para saber aproximadamente a quantos quilômetros 5 milhas correspondem, pega-se o número de Fibonacci correspondendo ao número de milhas (5) e olha-se para o número seguinte (8). 5 milhas são aproximadamente 8 quilômetros. Esse método funciona porque, por coincidência, o fator de conversão entre milhas e quilômetros (1.609) é próximo de φ (1.618) (obviamente ele só é útil para aproximações bem grosseiras: além do factor de conversão ser diferente de φ, a série converge para φ).
Em música os números de Fibonacci são utilizados para a afinação de instrumentos ou como nas artes visuais, determinar proporções entre elementos formais. Um exemplo é a Música para Cordas, Percussão e Celesta de Béla Bartók.
Le Corbusier usou a seqüência de Fibonacci na construção do seu modulor, um sistema de proporções baseadas no corpo humano e aplicadas ao projeto de arquitetura.
Conclusão:
Conclui-se que a matemática e a geometria tem sido estudada e aplicada na Odontologia e na Arte desde a antiguidade por artistas,pintores,matemáticos, geometras,engenheiros e arquitetos. E em nossos dias, médicos e Cirurgiões Dentistas buscam uma harmonia entre os dentes e a face do homem. além do número Áureo ser uma constante no crescimento dos seres vivos como demonstraram vários autores.
Conclusion: it is Ended that the mathematics and the geometry has been studied and applied in the Dentistry and in the Art from the antiquity for artists, painters, mathematical, geometricians, engineers and architects. And in our days, doctors and Surgeons Dentistas look for a harmony between the teeth and the man's face. besides the number Áureo to be a constant in the alive beings' growth as they demonstrated several authors.
Bibliografia:
1. Berry FH. Is the theory of temperament of foundation of the study of prosthetic art. Dent Mag, v.1, p.405-13 – 1906.
2. BICHARA, S.E. Et all. Comparisons of mesiodistal and buccolingual crown dimensions of the permanent teeth in three from Egypth, México and the United States. AM J. Orthop., St. Louis, v.96, n.5, p.416-422, nov. 1989.
3. BOLTON, W. Disharmony in tooth size and its relation to the analysis and treatament of malloclusion Am. J. Orthod., v.28, n. 3, p. 113 – 130, Julho de 1958
4. CONCEIÇÃO E.N., Dentística, Saúde e estética. Editora Artemed: 2000.
5. DAS NEVES, J.B., Implantodontia oral: otimização estética: uma abordagem dos tecidos moles e duros. Editora Gráfica Rona Editora São Paulo, 2001.
6. Oliveira, V.L.R., Estudo da proporção áurea entre incisivos centrais. SOTAU R. Virtual odontol. 2008. 2 (5): 2-6.
7. Ricketts RM. The biologic signicance of the divine proportion and Fibonacci series. Am J Ortho. 1982. May; 81(5): 351- 370.
8. Santos, Alfredo A., Aulas de Anatomia Artística - ICS - UFBA. 1980.
9. Tjan, A.H.L., Miller, G.D. ; the, J>G.P.; Some estetic factores in smile J. prosthed Dent , v. 5, n. 1, p. 24-28, jan. 1984.
10. [Link] http://www.terramater.pt/
11.[Link]: http://www. pt.wikipedia.org/wiki/Biometria.
12.[Link]: http:// www.malima.com.br/article_read.asp.
13.[Link]:http://www. pessoal.sercomtel.com.br/matematica/alegria/fibonacci/seqfib2.
14.[Link]:pt.wikipedia.org/wiki/Número_de_Fibonacci.
15. Y. Matiyasevich. "Enumerable sets are Diophantine." Doklady Akademii Nauk SSSR,
191, pp. 279-282, 1970. English translation in Soviet Mathematics. Doklady, vol.
11, no. 2, 1970.
16. M. Davis. "Hilbert's Tenth Problem is Unsolvable." American Mathematical Monthly
80, pp. 233-269, 1973.


















Nenhum comentário:
Postar um comentário